Next: About this document ...
Research activities in condensed matter theory spanned diverse areas such as
the physics of nanomaterials, mesoscopic systems, molecular motors, heavy
fermion systems, nonlinear Schrodinger equation, complex systems namely
unzipping of DNA, sandpile models etc., phase transition in 2D extended
XY-spin model, and electronic properties of hetero-structures. More
specifically, Raman scattering intensity has been calculated for nano
structures to study the interplay of the electronic and vibrational
properties of such systems. The structure and stability of atomic clusters
has been studied. Studies have been performed of the interplay of
antiferromagnetism and superconductivity in heavy fermion systems and
correlated superconductors. In mesoscopic systems at equilibrium, current
enhancement effects have been demonstrated. Dephasing in mesoscopic systems,
specifically in the Aharonov-Bohm ring, has been studied. Using stochastic
energetics method, the efficiency of frictional thermal ratchets (molecular
motors) has been studied.
The dynamics of phase transition associated with the unzipping of DNA has
been studied using a discrete lattice model. The time evolution of unzipping
is found to obey scaling laws, and the relevant dynamic exponents have been
determined. Studies have been made of the universality class of noisy pulled
fronts. Interfacial fluctuations in a sandpile have been studied as a
limiting case of a class of one dimensional self-organized critical models.
Studies have been made of certain discrete nonlinear Schrodinger equations
and propagating solitary solutions have been shown to exist in such systems.
The symmetry properties of these equations have been studied. Dark Current
in AlGaAs/GaAs based hetero-structures has been studied, and different
processes responsible for the escape of electrons from a biased single
rectangular quantum well based on the Al Ga
Ga As/GaAs
heterojunctions have been considered. Investigations have been performed of
the first-order transition in the classical 2D extended XY-spin model using
Monte Carlo simulations and it has been demonstrated that the energy as a
function of temperature exhibits a `S'-shape at the first-order transition.
As/GaAs
heterojunctions have been considered. Investigations have been performed of
the first-order transition in the classical 2D extended XY-spin model using
Monte Carlo simulations and it has been demonstrated that the energy as a
function of temperature exhibits a `S'-shape at the first-order transition.
S. N. Behera
Atomic clusters, cluster assembled materials and nanostructures in
general: Collaborative work on both the theoretifcal and experimental
aspects of cluster assembled nanomaterials has been carried out duirng the
year under consideration.
One of the most important aspects of physics of nanomaterials is determining
their electronic as well as lattice vibrational properties. Since these
nanomaterials quite often manifest as low dimensional systems such as
quantum wires and quantum dots it is possible that these exhibit a strong
interplay of their electronic and vibrational properties. Such an interplay
is expected to be seen experimentally in metallic quantum nanowires and
carbon nanotubes with diameters of a few nanometers and lengths extending to
microns. These being one dimensional metallic systems, their electronic
collective excitations, the plasmons are known to exhibit accoustic and
optical like branches. The optical plasmons can have frequencies at the zone
centre which are comparable to the optical phonons. Hence in a Raman
scatterning experiment it is possible to study the interplay of these two
modes. Keekping this in mind the Raman scatterning intensity is calculated
which predicts clearly such an interplay between the two modes.
In the case of atomic clusters their structure and stability is determined
by the electronic structure. Earlier a parametrized orthogonal tight binding
molecular dynamics simulation method was adopted to calculate the structure
and stability of samall silicon clusters consisting of upto 19 atoms. In
order to check the reliability of these calculations, the results are
compared with those obtained from other methods.
A phonomenological liquid drop model of nanoparticle is used to explain the
lattice contraction of nanometer sized Sn and Bi particles.
Interplay of Magnetism and super-conductivity in Heavy Fermion
Systems and correlated superconductors: The study of the interplay of
magnetism and superconductivity is probably as old as the discovery of
superconductivity itself. However, the coexistance of antiferromagnetism and
superconductivity in systems like Rare earth Rhodium Borides and other
ternary compounds dates back to about three decades. Subsequently the same
coexistence was also found in some heavy fermion syperconductors, organic
superconductors and more recently in Rare earth Nickel Borocarbide. The
interplay, of these two long range orders, is probably at its best in these
Borocarbides because of the availability of systems in which the
superconducting (T and antiferromagnetic (T
and antiferromagnetic (T ordering
transition temperatures are close to each other. These anomalies manifest as
suppression of T
ordering
transition temperatures are close to each other. These anomalies manifest as
suppression of T on alloying as anomolous temperature dependence of
the upper critical field and also in the temperature dependence of the
phonon spectra as observed by inelastic neutron scattering. In order to
understand these anomalies, a model (proposed earlier for explaining the
observed heavy fermnion behaviour of certain high T
on alloying as anomolous temperature dependence of
the upper critical field and also in the temperature dependence of the
phonon spectra as observed by inelastic neutron scattering. In order to
understand these anomalies, a model (proposed earlier for explaining the
observed heavy fermnion behaviour of certain high T superconductors)
was adopted for the borocarbides. The model accounts for staggered
sub-lattice antiferromagnetism and superconductivity by the itenerant
conduction electrons, arising from the transition metal atoms; while the
heavy fermion like behaviour is accounted for by the localized f-level of
the rare-earth atom hybridizing with the itinerant electrons. The interplay
of antiferromagnetism (AFM) and superconductivity (SC) was investigated by
studying the temperature dependence of the respective order parameters. For
a suitable choice of the parameters, the temperature dependence of the
superconducting order parameter exhibits features similar to that observed
in the temperature dependence of the upper critical field of some
borocarbide superconductors in which AFM and SC coexist.
Theoretical calculations are performed of the Raman spectra of some heavy
fermion superconductors. The system is represented by the Periodic Anderson
Model, to account for the heavy fermion behaviour to which a mean field BCS
term is added to represent superconductivity. Besides, the electrons are
coupled to the phonons through the hybridization as well as the localized
orbitaals. A detailed study of the Raman intensities and their variation
with varying parameters of the model is presented. The study also provides a
detailed review of the properties of heavy fermion, Kondo lattice and Kondo
insurating systems.
superconductors)
was adopted for the borocarbides. The model accounts for staggered
sub-lattice antiferromagnetism and superconductivity by the itenerant
conduction electrons, arising from the transition metal atoms; while the
heavy fermion like behaviour is accounted for by the localized f-level of
the rare-earth atom hybridizing with the itinerant electrons. The interplay
of antiferromagnetism (AFM) and superconductivity (SC) was investigated by
studying the temperature dependence of the respective order parameters. For
a suitable choice of the parameters, the temperature dependence of the
superconducting order parameter exhibits features similar to that observed
in the temperature dependence of the upper critical field of some
borocarbide superconductors in which AFM and SC coexist.
Theoretical calculations are performed of the Raman spectra of some heavy
fermion superconductors. The system is represented by the Periodic Anderson
Model, to account for the heavy fermion behaviour to which a mean field BCS
term is added to represent superconductivity. Besides, the electrons are
coupled to the phonons through the hybridization as well as the localized
orbitaals. A detailed study of the Raman intensities and their variation
with varying parameters of the model is presented. The study also provides a
detailed review of the properties of heavy fermion, Kondo lattice and Kondo
insurating systems.
S.M.Bhattacharjee
Dynamics of Unzipping of DNA by force: It is now well established
that unzipping of DNA by a force is a genuine phase transition. A double
stranded DNA remains bound until the force exceeds a critical value.
The dynamics of this unzipping transition has been studied using a discrete
lattice model for DNA. The analytical solution of the equilibrium behaviour
gives the phase diagram of the model exactly. The dynamics of unzipping can
then be studied in various phases and also on the phase boundary. The time
evolution of unzipping is found to obey scaling laws.
The relevant ``dynamic'' exponents have been determined. These scalings can
be understood from the plausible mechanisms of unzipping and denaturation,
except for the very high temperature region. For example, on the phase
boundary, the time scales for unzipping one base pair at the contact point
should be the same as the time required for the new kink released to diffuse
out of the unzipped strand. This then tells us that the length m(t) of the
unzipped strand should grow with time t as m(t) t
t . Since
the scaling form depends on the thermodynamic phase of the system, it could
play a role in the mechanism to separate unzipped region from thermally
denatured regions in real systems.
. Since
the scaling form depends on the thermodynamic phase of the system, it could
play a role in the mechanism to separate unzipped region from thermally
denatured regions in real systems.
A. M. Jayannavar
Thermal ratchets (Molecular motors): It is known that molecular
motors extract energy out of nonequilibrium enviroment and perform useful
work (carrying cargo). Moreover they move in a unidirectional motion in
absence of bias, which is ruled out under thermal equilibrium condition.
Molecular motors thus acts as a engines, rectifying fluctuations into work.
It is therefore necessary to quantify the efficiency of these engines
working away from equilibrium (unlike conventional heat engines,
fluctuations play the primary role).
For this we studied the efficiency of frictional thermal ratchets (motors)
using stochastic energetics method, driven by finite frequency driving force
and in contact with a heat bath. The efficiency exhibits varied behavior
with driving frequency. Both nonmonotonic and monotonic behavior have been
observed. Unlike the conventional heat engines, the magnitude of efficiency
of thermal ratchets in finite frequency regime may be more than the
efficiency in the adiabatic regime.
We are also studying the motion of two coupled overdamped Brownian motors
moving in a flashing ratchet type potential. Besides the theoretical
interest of studying the rectification properties of more complex system
over a single particle system, these models have direct relevance to motion
of double headed kinesin moving along cytoskeleton filaments. Coupled
systems show several features like enhancement of diffusion and currents,
noise induced stability, negative resistance, anomolous hysterisis, etc.
Time in Quantum mechanics: The subject of time in quantum mechanics
is of perennial interest especially because there is no observable for the
time taken by a particle to transmit (or reflect) from a given region of
interest.The problem is essentially due to the fact that there is no
hermitian operator to calculate this time in quantum mechanics. This problem
has been beset with a lot of controversies. Several methods have been
proposed based on scattering phase shifts and using different quantum
clocks, where the time taken is clocked by some external input or indirectly
from the phase of the scattering amplitudes. In our work we give a general
method for calculating conditional sojourn times based on wave attenuation.
In this approach clock mechanism does not couple to the Hamiltonian of the
system. We emphasize that this time should satisfy certain criteria, which
are -(a) It should be real, (b) It should add up for non-overlapping
regions, (c) It should be causally related to the region of interest and (d)
tend to correct classical limits. Our proposed clock satisfies all these
aforesaid criteria as opposed to several earlier studies.
We have obtained an expression for the conditional time for the reflection
of a wave from an arbitrary potential barrier using the WKB wavefunction in
the barrier region. For this we have used the analogy with Bohmian picture
of quantum mechanics. Our result indicates that the conditional times for
transmission and reflection are equal for a symmetric barrier within the
validity of the WKB approach.
Current enhancement effect in mesoscopic systems at
equilibrium: We have studied a multiply connected mesoscopic system
in both its open and closed form variations but in equilibrium using
quantum theory. This system exhibits remarkable features, in its open
form variation we see current enhancement, hitherto seen only in
non-equilibrium systems in absence of magnetic flux. In its closed
form analog parity effects are broken. Further we have analysed the
global and local current densities of our system and shown that the
orbital magnetic response of the system calculated from the current
densities (and inherently linked to the topological configuration) is
qualitatively not same as that calculated from its eigenenergy spectra
or from theory of equilibrium statistical mechanics.
Dephasing in mesoscopic physics: The Aharonov-Bohm ring has
been the mainstay of mesoscopic physics research since its
inception. In our work we have dwelt on the problem of dephasing of AB
oscillations using a model based on stochastic absorption. Dephasing
or decoherence implies the loss of quantum mechanical interference due
to coupling of an interfering particle with its surrounding
environment. Complete dephasing erases the interference pattern. Thus
quantum mechanical system behaves as though it were described by
classical probability theory. We have calculated the conductance of
Aharonov-Bohm ring by reformulating sequential transport. We have
shown that conductance is symmetric under flux reversal (Onsager's
relation) and visibility of AB oscillations decay to zero as a
function of the incoherence parameter thus signalling dephasing in the
system. We also see that this method of stochastic absorption/wave
attenuation is better than the optical potential model which has also
been used to simulate dephasing.
K. Kundu
Solitary Wave Like Solutions In Discrete Nonlinear Schödinger
Equations: A new set of 1D discrete nonlinear Schrödinger Hamiltonians
is introduced which includes the Ablowitz-Ladik system as a limit. The
symmetry properties of these systems and their relationship with the
Davydov-Holstein models for transport in biophysical systems are discussed.
Proposed models are shown to possess propagating localized solutions. These
propagating solutions exhibit nontrivial interactions, and, therefore, do
not have the usual soliton properties.
A Study Of A New Class Of Discrete Nonlinear Schrödinger
Equations: A new class of 1D discrete nonlinear Schrödinger
Hamiltonians with tunable nonlinerities is introduced, which includes the
integrable Ablowitz-Ladik system as a limit. A new subset of equations,
which are derived from these Hamiltonians using a generalized definition of
Poisson brackets, and collectively refered to as the N-AL equation, is
studied. The symmetry properties of the equation are discussed. These
equations are shown to possess propagating localized solutions, having the
continuous translational symmetry of the one-soliton solution of the
Ablowitz-Ladik nonlinear Schrödinger equation. The N-AL systems are
shown to be suitable to study the combined effect of the dynamical imbalance
of nonlinearity and dispersion and the Peierls-Nabarro potential, arising
from the lattice discreteness, on the propagating solitary wave like
profiles. A perturbative analysis shows that the N-AL systems can have
discrete breather solutions, due to the presence of saddle center
bifurcations in phase portraits. The unstaggered localized states are shown
to have positive effective mass. On the other hand, large width but small amplitude
staggered localized states have negative effective mass. The collison
dynamics of two colliding solitary wave profiles are studied numerically.
Notwithstanding colliding solitary wave profiles are seen to exhibit
nontrivial nonsolitonic interactions, certain universal features are
observed in the collison dynamics. Future scopes of this work and possible
applications of the N-AL systems are discussed.
There is at least one continuous nonlinear equation,  equation, which can have either solitary wave solutions or ``kink-like''
solutions with permanent profile. On the contary, to the best of my
knowledge there is no known analogy of
equation, which can have either solitary wave solutions or ``kink-like''
solutions with permanent profile. On the contary, to the best of my
knowledge there is no known analogy of  type of equation in
the discrete case. So, here an extended nonintegrable version of the
Ablowitz-Ladik discrete nonlinear Schrödinger equation (ALDNLSE), with a
"tunable" nonlinearity is proposed. The
form of nonlinearity in this equation is such that it can allow solitary
wave like solutions, as seen in
type of equation in
the discrete case. So, here an extended nonintegrable version of the
Ablowitz-Ladik discrete nonlinear Schrödinger equation (ALDNLSE), with a
"tunable" nonlinearity is proposed. The
form of nonlinearity in this equation is such that it can allow solitary
wave like solutions, as seen in  equation. This equation for
m
equation. This equation for
m  Z is
Z is
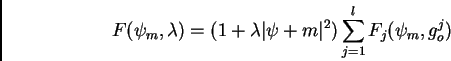 |
(1) |
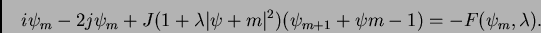 |
(2) |
When  , the system has an extra nearest-neighbor coupling in hopping with
coupling constant, . In the
, the system has an extra nearest-neighbor coupling in hopping with
coupling constant, . In the
 limit, this particular form
of nonlinearity can be obtained by using the standard off-diagonal
quasiparticle-phonon interaction theory and an antiadiabatic approximation.
This equation also has an intimate relationship with Davydov-Holstein models
for transport in biophysical systems.
The new discrete nonlinear Schrödinger equation enables us to show the
existence of discrete nonintegrable nonlinear equations which can allow
certain localized states to travel without experiencing any Peierls-Nabarro
pinning from the lattice discreteness. It is also found that at least the
interaction of two soliton-like solutions in nonintegrable systems has
universal features. On the whole, this study offers a very significant
insight into the transport properties of the well known Davydov-Holstein
model for biological transport, and transport properties of localized states
in soft molecular chains.
limit, this particular form
of nonlinearity can be obtained by using the standard off-diagonal
quasiparticle-phonon interaction theory and an antiadiabatic approximation.
This equation also has an intimate relationship with Davydov-Holstein models
for transport in biophysical systems.
The new discrete nonlinear Schrödinger equation enables us to show the
existence of discrete nonintegrable nonlinear equations which can allow
certain localized states to travel without experiencing any Peierls-Nabarro
pinning from the lattice discreteness. It is also found that at least the
interaction of two soliton-like solutions in nonintegrable systems has
universal features. On the whole, this study offers a very significant
insight into the transport properties of the well known Davydov-Holstein
model for biological transport, and transport properties of localized states
in soft molecular chains.
S. G. Mishra
Dark Current in AlGaAs/GaAs Based Hetero-structures:
Long-wavelength infrared detectors, based on inter subband absorption in
quantum well structures are being rapidly developed. The efficiency of a
detector is high when the dark current in it is extremely small compared to
the photocurrent. In order to understand the key parameters for reducing the
dark current, it is essential to calculate it taking different escape
mechanisms which contribute to it.
Different processes responsible for the escape of electrons from a biased
single rectangular quantum well based on the Al Ga
Ga As/GaAs
heterojunctions have been considered. The direct tunneling rate due to the
barrier lowering as a result of the applied electric field is studied. It is
found to be temperature independent and exponential in nature. The indirect
tunneling rates due to interaction of carriers with collective modes in the
system are calculated using the Fermi golden rule where the interaction
Hamiltonians are expressed in Frohlich form. While the acoustic
phonon-assisted tunneling rate has negligible contribution at all field
strengths and temperatures, the optic phonon- and plasmon-assisted tunneling
rates turn out to be significant at room temperatures. While the phonon and
plasmon assisted tunneling currents are weak, the dark current is governed
by currents arising from the direct tunneling and thermionic processes.
As/GaAs
heterojunctions have been considered. The direct tunneling rate due to the
barrier lowering as a result of the applied electric field is studied. It is
found to be temperature independent and exponential in nature. The indirect
tunneling rates due to interaction of carriers with collective modes in the
system are calculated using the Fermi golden rule where the interaction
Hamiltonians are expressed in Frohlich form. While the acoustic
phonon-assisted tunneling rate has negligible contribution at all field
strengths and temperatures, the optic phonon- and plasmon-assisted tunneling
rates turn out to be significant at room temperatures. While the phonon and
plasmon assisted tunneling currents are weak, the dark current is governed
by currents arising from the direct tunneling and thermionic processes.
S. B. Ota
Microcanonical Monte Carlo Simulations: The first-order transition
in finite systems has induced notable scrutiny in recent years. Alder and
Wainwright were the first to report a `S'-shape in the phase-transition
region of a two-dimensional (2D) system consisting of 870 hard-disk
particles. Jellinek et al have simulated the solid-liquid phase change of 13
Argon particles using molecular dynamics. They have reported that when the
caloric curve is constructed from averages over a long run, its form is
smooth and monotonic showing no trace of the `loop' that is observed with
much shorter molecular dynamics run. The temperature dependence of energy
for these systems, however, shows a `S'-shape at the first-order transition
in many computer simulations in microcanonical ensemble. There is
substantial contemporary study on atomic clusters, in which, this element is
also manifested in the temperature dependence of system energy. It is,
however, not understood clearly, why the `S'-shape arises in first-order
transitions. Simulations in microcanonical ensemble implies that the system
is not in contact with a heat bath or explicitly: `isolated'. We have
investigated the first-order transition in the classical 2D extended XY-spin
model using Monte Carlo simulations. The simulations have been carried out
on a system with 100 spins in the microcanonical ensemble, which represents
a finite-isolated system. The energy as a function of temperature is found
to exhibit a `S'-shape at the first-order transition. We conclude that the
observed phenomena at the first-order transition should be interpreted as
the equilibrium response of a finite-isolated system.
G. Tripathy
Fluctuations of a pulled front: In continuation of an earlier work
suggesting that fronts propagating into an unstable state should not be in
the standard Kardar-Parisi-Zhang (KPZ) universality class, an effective
field equation for this class of problems is introduced. It is shown on the
basis of this equation that noisy pulled fronts in  bulk dimensions should
be in the universality class of the ((d+1)+1)D KPZ equation rather than the
bulk dimensions should
be in the universality class of the ((d+1)+1)D KPZ equation rather than the  KPZ
equation. Our scenario ties together a number of heretofor unexplained
results in the literature, and is supported by earlier numerical results.
Interfacial fluctuations in a sandpile: Surface fluctuations of the
Bak-Tang-Wiesenfeld (BTW) model were studied as a limiting case of a class
of one dimensional self-organized critical (SOC) models where the effect of
inertia is incorporated in a simple way. We find that for small systems the
nature of interfacial fluctuations are fully described by an appropriate
modification of the standard Kardar-Parisi-Zhang (KPZ) theory. However, we
also find that for larger systems roughness scales very differently from the
KPZ prediction. This indicates that criticality of the BTW model is
responsible for the anomalously large roughness exponent observed.
KPZ
equation. Our scenario ties together a number of heretofor unexplained
results in the literature, and is supported by earlier numerical results.
Interfacial fluctuations in a sandpile: Surface fluctuations of the
Bak-Tang-Wiesenfeld (BTW) model were studied as a limiting case of a class
of one dimensional self-organized critical (SOC) models where the effect of
inertia is incorporated in a simple way. We find that for small systems the
nature of interfacial fluctuations are fully described by an appropriate
modification of the standard Kardar-Parisi-Zhang (KPZ) theory. However, we
also find that for larger systems roughness scales very differently from the
KPZ prediction. This indicates that criticality of the BTW model is
responsible for the anomalously large roughness exponent observed.



Next: About this document ...
Condensed Matter Theory
2003-06-03